§ 49. Параллельное соединение проводников
Другой способ соединения проводников, применяемый в практике, называется параллельным соединением. На рисунке 79, а изображено параллельное соединение двух электрических ламп, а на рисунке 79, б — схема этого соединения. Обратите внимание на важные особенности такого соединения.
Рис. 79. Параллельное соединение лампочек
При параллельном соединении все входящие в него проводники одним своим концом присоединяются к одной точке цепи А, а вторым концом к другой точке В (см. рис. 79, б). Поэтому напряжение на участке цепи ЛВ и на концах всех параллельно соединённых проводников одно и то же:
U = U1 = U2.
Очень удобно поэтому применять параллельное соединение потребителей в быту и в технике, так как все потребители в этом случае изготавливаются в расчёте на одинаковое напряжение. Кроме того, при выключении одного потребителя другие продолжают действовать, ток в них не прерывается, так как цепь остаётся замкнутой.
При параллельном соединении ток в точке В (см. рис. 79, б) разветвляется на два тока I1 и I2» сходящиеся вновь в точке А, подобно тому как изображённый на рисунке 80 поток воды в реке распределяется по двум каналам, сходящимся затем вновь.
Рис. 80. Схожесть потока в реке с током в цепи
Поэтому сила тока в неразветвленной части цепи равна сумме сил токов в отдельных параллельно соединённых проводниках:
I = I1 + I2.
При параллельном соединении как бы увеличивается площадь поперечного сечения проводника. Поэтому общее сопротивление цепи уменьшается и становится меньше сопротивления каждого из проводников, входящих в цепь. Так, например, сопротивление цепи R, состоящей из двух одинаковых ламп, сопротивлением R1 каждая, в два раза меньше сопротивления одной лампы: R = R1 / 2 .
Общее сопротивление цепи при параллельном соединении проводников определяется по формуле
1 / R = 1 / R1 + 1 / R2
В одну и ту же электрическую цепь параллельно могут быть включены самые различные потребители электрической энергии. На рисунке 81 показано параллельное включение электрических ламп, нагревательных приборов и электродвигателя. Такая схема соединения потребителей тока используется, например, в жилых помещениях; в точках а и б провода осветительной сети вводятся в квартиру.
Рис. 81. Параллельное включение в цепь различных потребителей
Потребители, параллельно включаемые в данную сеть, должны быть рассчитаны на одно и то же напряжение, равное напряжению в сети.
Напряжение в сети, используемое у нас для освещения и в бытовых приборах, равно 220 В. Поэтому электрические лампы и различные бытовые электроприборы изготовляют на 220 В.
В практике часто применяется смешанное (последовательное и параллельное) соединение проводников.
Параллельное соединение двух ламп
Зная сопротивления проводников, соединённых параллельно, и напряжение на этом участке цепи, можно определить многие другие электрические величины этой цепи. Для этого нужно использовать формулы: U = U1 = U2 и I = I1 + I2, а также закон Ома для участка цепи.
Пример. В осветительную сеть комнаты включены две электрические лампы, сопротивления которых 200 и 300 Ом. Напряжение в сети 120В. Определить силу тока в каждой лампе, силу тока в подводящих проводах (т. е. силу тока до разветвления), общее сопротивление участка, состоящего из двух ламп. Запишем условие задачи и решим её.
Решив задачу, мы убедились, что общее сопротивление участка цепи R = 120 Ом, состоящего из двух параллельно соединённых проводников сопротивлением R1 = 200 Ом и R2 = 300 Ом, меньше сопротивления каждого проводника.
Вопросы
- Какое соединение проводников называют параллельным? Изобразите его на схеме.
- Какая из электрических величин одинакова для всех проводников, соединённых параллельно?
- Как выражается сила тока в цепи до её разветвления через силы токов в отдельных ветвях разветвления?
- Как изменяется общее сопротивление разветвления после увеличения числа проводников в разветвлении?
- Какое соединение проводников применяется в жилых помещениях? Какие напряжения используются для бытовых нужд?
Упражнение 33
- Два проводника сопротивлением 10 и 15 Ом соединены параллельно и подключены к напряжению 12 В. Определите силу тока в каждом проводнике и силу тока до разветвления.
- Почему бытовые приборы в помещении необходимо соединять параллельно?
- Три потребителя сопротивлением 20, 40, 24 Ом соединены параллельно. Напряжение на концах этого участка цепи 24 В. Определите силу тока в каждом потребителе, общую силу тока в участке цепи и сопротивление участка цепи.
- Два проводника имеют сопротивления 5 Ом и 500 Ом. Почему при последовательном соединении этих проводников их общее сопротивление будет больше 500 Ом, а при параллельном соединении меньше 5 0м?
- На рисунке 82 изображена схема смешанного соединения проводников, сопротивления которых: R1 = 4 Ом, R2 = 6 Ом, R3 = 12 Ом, R4 = 2 Ом. Амперметр показывает силу тока 1 А. Определите напряжение между точками В и С и силу тока в каждом проводнике.
Рис.
82
Источник: https://ansevik.ru/fizika_8/49.html
Соединение элементов в цепи переменного напряжения и тока
Всем доброго времени суток! В прошлой статье я рассказал о воздействии переменного напряжения на элементы цепи (сопротивление, индуктивность и ёмкость) и воздействие этих элементов на напряжение, ток и мощность. В данной статье я расскажу о последовательном и параллельном соединении элементов цепи и воздействии на такие цепи переменного напряжения и тока.
Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.
Последовательное соединение элементов цепи при переменном напряжении
Начнём с последовательного соединения сопротивления R, индуктивности L и ёмкости C и рассмотрим воздействие на неё переменного напряжения с частотой ω.
Последовательное соединение элементов цепи.
В данной цепи входное переменное напряжение U в соответствии со вторым законом Кирхгофа будет равно алгебраической сумме переменных напряжений на отдельных элементах
где UR, UL, UC – напряжение на элементах цепи, сопротивлении R, индуктивности L и ёмкости С, соответственно,
Im – амплитудное значение переменного тока.
Графическое изображение напряжений и токов на последовательно соединённых элементах цепи представлено ниже
Напряжения и токи при последовательном соединении.
Итоговое выражение является тригонометрической формой записи второго закона Кирхгофа для мгновенных напряжений и его можно переписать в виде
где R – активное сопротивление,
Х – реактивное сопротивление.
Значение активного сопротивления R всегда только положительно, а реактивное сопротивление Х может принимать, как положительное значение Х > 0, тогда оно имеет индуктивный характер, так и отрицательное значение X < 0, в этом случае реактивное сопротивление имеет ёмкостный характер.
В случае же нулевого значения реактивного сопротивления, имеет место резонанс напряжений
В этом случае сопротивление цепи представлено только активной нагрузкой R, а следовательно сдвиг фаз между напряжением и током будет нулевым.
При расчётах нас интересует не столько ток и напряжение на отдельных элементах, сколько ток и напряжение всей цепи. Для этого продолжим преобразовывать напряжение
где Z – полное сопротивление цепи,
ψ – разность фаз между напряжением и током.
Таким образом, амплитудное значение напряжения Um и амплитудное значение тока Im связаны между собой следующим соотношением
где Um – амплитудное значение переменного напряжения,
Im – амплитудное значение переменного тока,
Z – полное сопротивление цепи.
Параллельное соединение элементов цепи при переменном напряжении
Теперь рассмотрим параллельное соединение элементов цепи (сопротивления, индуктивности и ёмкости) и прохождение по ним переменного тока.
Параллельно соединение элементов цепи.
Подадим на вход такой цепи переменное напряжение U, тогда электрический ток в цепи I, в соответствии с первым законом Кирхгофа, будет равняться алгебраической суммы токов проходящей через элементы цепи
IR, IL, IC – токи в элементах цепи, сопротивлении R, индуктивности L и ёмкости С, соответственно,
Um – амплитудное значение переменного тока.
Графическое изображение напряжений и токов в параллельно соединённых элементах цепи представлено ниже
Напряжение и токи при параллельном соединении.
Аналогично второму закону Кирхгофа, для первого закона также существует тригонометрическая форма записи, которая соответствует получившемуся выражению. Выполним ещё одно преобразование данного выражения
где g – активная проводимость, b – реактивная проводимость.
Как видно из формулы, реактивная проводимость может быть положительной b > 0, тогда она имеет индуктивный характер, а может быть отрицательной b < 0, тогда реактивная проводимость имеет ёмкостный характер. А активная проводимость может быть только положительной.
Отдельный случай представляет собой реактивная проводимость равная нулю, то есть в этом случае проводимость индуктивности и ёмкости одинаковы
Такой случай называется резонансом токов, в этом случае общая проводимость будет определяться только активной проводимостью, а сдвиг фаз между напряжением и током в цепи будет нулевым.
Определим зависимость между напряжением и силой тока в параллельной цепи
где y – полная проводимость,
ψ – разность фаз между напряжением и током в цепи.
Тогда зависимость между напряжением и током в цепи с параллельно соединёнными элементами будет иметь вид
где Um – амплитудное значение переменного напряжения,
Im – амплитудное значение переменного тока,
y – полная проводимость цепи.
Чему равна мощность в цепи при синусоидальном напряжении?
Мощность является основной энергетической характеристикой, поэтому рассмотрим мощность в цепи переменного напряжения. Мгновенная мощность в цепи будет равна
Как видно из получившегося выражения, мгновенная мощность состоит из постоянной составляющей UIcos(φ) и переменной составляющей UIcos(2ωt – φ), изменяющейся с удвоенной частотой по сравнению с частотой напряжения (тока).
Теперь определим среднее значение мощности за период или активную мощность, которая будет равна
где U – действующее значение переменного напряжения,
I – действующее значение переменного тока,
cos(φ) – коэффициент мощности.
Таким образом, активная мощность в цепи переменного напряжения (тока), равна произведению действующих значений напряжения и тока на коэффициент мощности.
При разработке и проектировании цепей переменного напряжения стараются сделать коэффициент мощности как можно больше, в идеале должен быть равен единице cos(φ) = 1. При небольших значениях данного коэффициента для создания в цепи необходимой мощности Р необходимо повышать величину напряжения U (тока I).
Теория это хорошо, но без практического применения это просто слова.Здесь можно всё сделать своими руками.
Источник: http://www.electronicsblog.ru/silovaya-elektronika/soedinenie-elementov-v-cepi-peremennogo-napryazheniya-i-toka.html
Закон ома параллельное и последовательное соединение проводников
В электрических цепях элементы могут соединяться по различным схемам, в том числе они имеют последовательное и параллельное соединение.
Последовательное соединение
При таком соединении проводники соединяются друг с другом последовательно, то есть, начало одного проводника будет соединяться с концом другого. Основная особенность данного соединения заключается в том, что все проводники принадлежат одному проводу, нет никаких разветвлений. Через каждый из проводников будет протекать один и тот же электрический ток. Но суммарное напряжение на проводниках будет равняться вместе взятым напряжениям на каждом из них.
Рассмотрим некоторое количество резисторов, соединенных последовательно. Так как нет разветвлений, то количество проходящего заряда через один проводник, будет равно количеству заряда, прошедшего через другой проводник. Силы тока на всех проводниках будут одинаковыми. Это основная особенность данного соединения.
Это соединение можно рассмотреть иначе. Все резисторы можно заменить одним эквивалентным резистором.
Ток на эквивалентном резисторе будет совпадать с общим током, протекающим через все резисторы. Эквивалентное общее напряжение будет складываться из напряжений на каждом резисторе. Это является разностью потенциалов на резисторе.
Если воспользоваться этими правилами и законом Ома, который подходит для каждого резистора, можно доказать, что сопротивление эквивалентного общего резистора будет равно сумме сопротивлений. Следствием первых двух правил будет являться третье правило.
Применение
Последовательное соединение используется, когда нужно целенаправленно включать или выключать какой-либо прибор, выключатель соединяют с ним по последовательной схеме. Например, электрический звонок будет звенеть только тогда, когда он будет последовательно соединен с источником и кнопкой.
Согласно первому правилу, если электрический ток отсутствует хотя бы на одном из проводников, то его не будет и на других проводниках. И наоборот, если ток имеется хотя бы на одном проводнике, то он будет и на всех других проводниках. Также работает карманный фонарик, в котором есть кнопка, батарейка и лампочка.
Все эти элементы необходимо соединить последовательно, так как нужно, чтобы фонарик светил, когда будет нажата кнопка.
Иногда последовательное соединение не приводит к нужным целям. Например, в квартире, где много люстр, лампочек и других устройств, не следует все лампы и устройства соединять последовательно, так как никогда не требуется одновременно включать свет в каждой из комнат квартиры. Для этого последовательное и параллельное соединение рассматривают отдельно, и для подключения осветительных приборов в квартире применяют параллельный вид схемы.
Параллельное соединение
В этом виде схемы все проводники соединяются параллельно друг с другом. Все начала проводников объединены в одну точку, и все концы также соединены вместе. Рассмотрим некоторое количество однородных проводников (резисторов), соединенных по параллельной схеме.
Этот вид соединения является разветвленным. В каждой ветви содержится по одному резистору. Электрический ток, дойдя до точки разветвления, разделяется на каждый резистор, и будет равняться сумме токов на всех сопротивлениях. Напряжение на всех элементах, соединенных параллельно, является одинаковым.
Все резисторы можно заменить одним эквивалентным резистором. Если воспользоваться законом Ома, можно получить выражение сопротивления. Если при последовательном соединении сопротивления складывались, то при параллельном будут складываться величины обратные им, как записано в формуле выше.
Работа тока
Последовательное и параллельное соединение, рассмотренное ранее, было справедливо для величин напряжения, сопротивления и силы тока, являющихся основными. Работа тока определяется по формуле:
А = I х U х t, где А – работа тока, t – время течения по проводнику.
Для определения работы при последовательной схеме соединения, необходимо заменить в первоначальном выражении напряжение. Получаем:
А=I х (U1 + U2) х t
Раскрываем скобки и получаем, что на всей схеме работа определяется суммой на каждой нагрузке.
Точно также рассматриваем параллельную схему соединения. Только меняем уже не напряжение, а силу тока. Получается результат:
А = А1+А2
Мощность тока
При рассмотрении формулы мощности участка цепи снова необходимо пользоваться формулой:
Источник: https://vemiru.ru/info/zakon-oma-parallelnoe-i-posledovatelnoe-soedinenie/
Последовательное и параллельное соединение. Применение и схемы
В электрических цепях элементы могут соединяться по различным схемам, в том числе они имеют последовательное и параллельное соединение.
Влияние схемы соединения на новогоднюю гирлянду
После перегорания одной лампы в гирлянде можно определить вид схемы соединения. Если схема последовательная, то не будет гореть ни одной лампочки, так как сгоревшая лампочка разрывает общую цепь. Чтобы выяснить, какая именно лампочка сгорела, нужно проверять все подряд. Далее, заменить неисправную лампу, гирлянда будет функционировать.
При применении параллельной схемы соединения гирлянда будет продолжать работать, даже если одна или несколько ламп сгорели, так как цепь не разорвана полностью, а только один небольшой параллельный участок. Для восстановления такой гирлянды достаточно увидеть, какие лампы не горят, и заменить их.
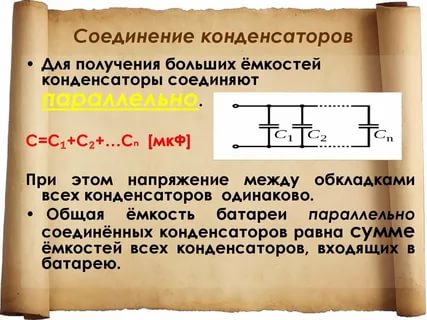
Последовательное и параллельное соединение для конденсаторов
При последовательной схеме возникает такая картина: заряды от положительного полюса источника питания идут только на наружные пластины крайних конденсаторов. Конденсаторы, находящиеся между ними, передают заряд по цепи. Этим объясняется появление на всех пластинах равных зарядов с разными знаками. Исходя из этого, заряд любого конденсатора, соединенного по последовательной схеме, можно выразить такой формулой:
qобщ= q1 = q2 = q3
Для определения напряжения на любом конденсаторе, необходима формула:
U= q/С
Где С — емкость. Суммарное напряжение выражается таким же законом, который подходит для сопротивлений. Поэтому получаем формулу емкости:
С= q/(U1 + U2 + U3)
Чтобы сделать эту формулу проще, можно перевернуть дроби и заменить отношение разности потенциалов к заряду емкости. В результате получаем:
1/С= 1/С1 + 1/С2 + 1/C3
Немного иначе рассчитывается параллельное соединение конденсаторов.
Общий заряд вычисляется как сумма всех зарядов, накопившихся на пластинах всех конденсаторов. А величина напряжения также вычисляется по общим законам. В связи с этим формула суммарной емкости при параллельной схеме соединения выглядит так:
С= (q1 + q2 + q3)/U
Это значение рассчитывается как сумма каждого прибора в схеме:
С=С1 + С2 + С3
Смешанное соединение проводников
В электрической схеме участки цепи могут иметь и последовательное и параллельное соединение, переплетающихся между собой. Но все законы, рассмотренные выше для отдельных видов соединений, справедливы по-прежнему, и используются по этапам.
Сначала нужно мысленно разложить схему на отдельные части. Для лучшего представления ее рисуют на бумаге. Рассмотрим наш пример по изображенной выше схеме.
Удобнее всего ее изобразить, начиная с точек Б и В. Они расставляются на некотором расстоянии между собой и от края листа бумаги. С левой стороны к точке Б подключается один провод, а справа отходят два провода. Точка В наоборот, слева имеет две ветки, а после точки отходит один провод.
Далее нужно изобразить пространство между точками. По верхнему проводнику расположены 3 сопротивления с условными значениями 2, 3, 4. Снизу будет идти ток с индексом 5. Первые 3 сопротивления включены в схему последовательно, а пятый резистор подключен параллельно.
Остальные два сопротивления (первый и шестой) подключены последовательно с рассматриваемым нами участком Б-В. Поэтому схему дополняем 2-мя прямоугольниками по сторонам от выбранных точек.
Теперь используем формулу расчета сопротивления:
- Первая формула для последовательного вида соединения.
- Далее, для параллельной схемы.
- И окончательно для последовательной схемы.
Аналогичным образом можно разложить на отдельные схемы любую сложную схему, включая соединения не только проводников в виде сопротивлений, но и конденсаторов. Чтобы научиться владеть приемами расчета по разным видам схем, необходимо потренироваться на практике, выполнив несколько заданий.
Похожие темы:
Источник: https://electrosam.ru/glavnaja/jelektrotehnika/raschjoty/posledovatelnoe-i-parallelnoe-soedinenie/
Последовательное и параллельное соединение резисторов
Последовательное соединение – это соединение двух или более резисторов в форме цепи, в которой каждый отдельный резистор соединяется с другим отдельным резистором только в одной точке.
Общее сопротивление Rобщ
При таком соединении, через все резисторы проходит один и тот же электрический ток. Чем больше элементов на данном участке электрической цепи, тем «труднее» току протекать через него. Следовательно, при последовательном соединении резисторов их общее сопротивление увеличивается, и оно равно сумме всех сопротивлений.
Напряжение при последовательном соединении
Напряжение при последовательном соединении распределяется на каждый резистор согласно закону Ома:
Т.е чем большее сопротивление резистора, тем большее напряжение на него падает.
Параллельное соединение резисторов
Параллельное соединение – это соединение, при котором резисторы соединяются между собой обоими контактами. В результате к одной точке (электрическому узлу) может быть присоединено несколько резисторов.
Напряжение при параллельном соединении
Напряжение между точками A и B является как общим напряжением для всего участка цепи, так и напряжением, падающим на каждый резистор в отдельности. Поэтому при параллельном соединении на все резисторы упадет одинаковое напряжение.
Электрический ток при параллельном соединении
Через каждый резистор течет ток, сила которого обратно пропорциональна сопротивлению резистора. Для того чтобы узнать какой ток течет через определенный резистор, можно воспользоваться законом Ома:
Смешанное соединение резисторов
Смешанным соединением называют участок цепи, где часть резисторов соединяются между собой последовательно, а часть параллельно. В свою очередь, смешанное соединение бывает последовательного и параллельного типов.
Параллельное соединение сопротивлений
Вместе с последовательным и смешанным соединениями сопротивлений существует параллельное соединение сопротивлений. Давайте разберем этот вид соединения.
При параллельном способе соединения, как следует из самого определения, сопротивления соединяются параллельно. Такое название получилось по той причине, что на принципиальной электрической схеме все сопротивления соединенные таким способом образуют ветви и эти ветви можно изобразить параллельными.
Как же соединяются сопротивления при параллельном способе. Допустим мы желаем подключить к источнику постоянного тока, пусть это будет аккумулятор 12 Volt, несколько ламп накаливания. Для того чтобы подключить их параллельно, нам надо по отдельности каждую лампу запитать от клемм аккумулятора.
При последовательном способе мы бы подключали каждую лампу друг к другу тем самым образовав своеобразную гирлянду, а при параллельном способе каждая лампа имеет свой персональный доступ к источнику напряжения.
Можно сказать, что все сопротивления (лампы) запитаны или подключены к одному и тому же напряжению.
Если при последовательном соединении у нас по сути образуется одна единственная ветвь электрической цепи (гирлянда), которая запитана от источника тока, то при параллельном соединении у нас много ветвей и все они запитаны от одного источника.
Визуально на принципиальной электрической схеме все ветви будут соединятся в одной точке и эта точка может выглядеть очень по разному для удобства представления схемы. Совершенно не обязательно, что все ветви сойдутся в одной точке на схеме, точка (узел) может быть как бы «растянута» до другой точки. Самое важное тут — это ветви и в этих ветвях протекает ток, причём в каждой ветви свой. Это важный признак параллельного соединения проводников — наличие ветвей.
Точки соединения ветвей также называют узлами или точками разветвления. Так называемые узлы на деле могут являться соединительными шинами к которым подсоединяются провода.
Применяя Закона Ома можно сделать следующие выводы:
Величина силы тока при параллельном соединении
При параллельном соединении к каждой ветви прикладывается одинаковое напряжение известной величины и в соответствии с Законом Ома ток будет равен напряжению делённому на сопротивление ветви. Допустим если напряжение 100 Вольт, а сопротивление 25 Ом, тогда ток ветви будет равен 4 Ампер. Если в другой ветви сопротивление в два раза больше, то есть 50 Ом, тогда ток будет равен 2 Ампер, то есть в два раза меньше.
При параллельном соединении токи в ветвях обратно пропорциональны величине сопротивлений ветвей, или иначе говоря они прямо пропорциональны проводимости ветвей. Чем меньшее сопротивление ветви, тем больший ток будет в ней протекать.
Суммарный ток всей цепи будет равен сумме токов всех ветвей этой цепи. По мере подключения новых ветвей суммарный ток будет становится всё больше и больше. Обычная розеточная сетевая колодка или попросту говоря «удлинитель» — типичный пример параллельного подключения проводников.
Когда в розетку удлинителя включают очередной электрический прибор — это и будет ветвь, следующая розетка и подключение — еще одна ветвь и т. д. Токи каждой ветви будут суммироваться.
Если удлинитель рассчитан на 16 Ампер нагрузки и дальше он скорее всего расплавится, то подключив в розетки скажем 5А+5А+3А+5А=18А будет явный перебор, хотя на каждый электроприбор будет подано общее сетевое напряжение 220 Вольт. Такие моменты надо учитывать.
Суммарное сопротивление при параллельном соединении
Иногда требуется найти общее сопротивление при параллельном соединении. К слову сказать в многоквартирном доме все потребители соединены параллельно с тем лишь различием, что электрическая сеть трёхфазная и ток переменный, а не постоянный. Но для такого случая также можно вычислить суммарное итоговое сопротивление.
Воспользовавшись Законом Ома можно вычислить ток в каждой ветви, затем можно вычислить суммарный ток, а затем, зная суммарный ток и приложенное напряжение можно легко вычислить общее сопротивление такого соединения.
В конечном итоге мы придём к выводу, что общая проводимость равна сумме проводимости всех ветвей цепи, а затем можно легко вычислить сопротивления, зная что проводимость — это величина обратная сопротивлению.
Если в каждой ветви одинаковое сопротивление, тогда задача упрощается. Чтобы вычислить общее сопротивление достаточно сопротивление ветви разделить на количество ветвей. Итоговая величина и будет общим сопротивлением. Если взять 10 сопротивлений по 50 Ом и соединить их параллельно, то общее сопротивление будет равно 50/10=5 Ом.
Последовательное и параллельное соединение ламп
Здравствуйте, уважаемые читатели сайта sesaga.ru. Сегодня мы рассмотрим практичные схемы последовательного и параллельного соединения ламп накаливания.
В статье схемы подключения трех и более ламп я рассказывал про параллельное соединение, а вот про последовательное упустил. В этой статье мы рассмотрим оба вида соединений используемых в быту.
Пойдем от простого к сложному. Обыкновенная лампа на принципиальных схемах обозначается таким образом:
Следующий момент Вы должны понять и запомнить:
Соединительные провода на схемах показываются линиями. Места соединения трех и более проводов показываются точками, а если провода пересекаются без соединения, то в месте их пересечения точка не ставится.
На рисунке ниже показано, когда провода просто пересекаются, то есть проходят рядом и не касаются друг друга, и когда провода уже соединены между собой — об этом говорит точка, стоящая в пересечении.
А теперь рассмотрим виды соединений:
Последовательное соединение ламп накаливания
Последовательное соединение ламп накаливания в домашнем быту используется редко. В свое время я подключал две лампы последовательно у себя в подъезде, но это был единичный случай.
Тут ситуация была такая, что подъездная лампа перегорала с периодичностью в один месяц, и надо было что-то делать.
Обычно, в таких случаях лампу включают через диод, чтобы она питалась пониженным напряжением 110В и долго служила. Вариант проверенный, но при этом сама лампа мерцает, да и светит в полнакала.
Когда же стоят две последовательно, то они так же питаются пониженным напряжением 110В, не мерцают, долго служат, светят и потребляют энергии как одна. Причем их можно развести по разным углам помещения, что тоже плюс.
Но повторюсь – это редкий случай.
Посмотрите на рисунок ниже. Здесь изображены две схемы последовательного соединения ламп накаливания. В верхней части рисунка показана принципиальная схема, а в нижней части – монтажная. Причем для лучшего восприятия, монтажная схема показана с реальным изображением ламп и двужильного провода.
Здесь в линии коричневого цвета, лампы HL1 и HL2 соединены последовательно – одна за другой. Поэтому такое соединение называют последовательным.
Если подать напряжение питания 220В на концы L и N, то загорятся обе лампы, но гореть они будут не в полную силу, а в половину накала. Так как сопротивление нитей ламп рассчитано на питающее напряжение 220В, и когда они стоят в цепи последовательно, одна за другой, то за счет добавления сопротивления нити накала следующей лампы, общее сопротивление цепи будет увеличиваться, а значит, для следующей лампы напряжение всегда будет меньше согласно закону Ома.
Поэтому при последовательном соединении двух ламп напряжение 220В будет делиться пополам, и составит 110В для каждой.
На следующем рисунке показаны три лампы соединенные последовательно.
На этой схеме напряжение на каждой лампе составит около 73 Вольт, так как будет делиться уже между тремя лампами.
Так же примером последовательного соединения могут служить новогодние гирлянды. Здесь из миниатюрных лампочек с низким питанием создается одна лампа на напряжение 220В.
Например, берем лампочки, рассчитанные на 6,3 Вольта и делим их на 220 Вольт. Получается 35 штук. То есть, чтобы сделать одну лампу на напряжение 220В, нам нужно соединить последовательно 35 штук с напряжением питания 6,3 Вольта.
P.S. Так как напряжение в сети не постоянно, то расчет лучше производить исходя из 245 – 250 Вольт.
Как Вы знаете, у гирлянд есть один недостаток. Перегорает одна из ламп, например, канала зеленого цвета, значит, не горит канал зеленого цвета. Тогда мы идем на базар, покупаем лампочки зеленого цвета, а потом дома по одной вынимаем, вставляем новую, и пока не заработает канал, перебираем его весь.
Вывод:
Недостатком последовательного соединения является то, что если выйдет из строя хоть одна из ламп, гореть не будут все, так как нарушается электрическая цепь.
А вторым недостатком, как Вы уже догадались, является слабое свечение. Поэтому последовательное соединение ламп накаливания на напряжение 220В в домашних условиях практически не применяется.
Параллельное соединение ламп
Параллельным соединением называют такое соединение, где все элементы электрической цепи, в данном случае лампы накаливания, находятся под одним и тем же напряжением. То есть получается, что каждая лампа, своими контактами, подключена и к фазе и к нулю. И если перегорит любая из ламп, то остальные будут гореть. Именно такое соединение ламп, рассчитанных на напряжение питания 220В, используется в домашнем быту, и не только.
На следующем рисунке так же изображено параллельное соединение. Здесь все три лампы соединены в одном месте. Еще такое соединение называют «звезда»
Бывают моменты, что когда именно из одной точки нужно развести проводку в разные направления.
Кстати, именно «звездой» делают разводку по квартире при монтаже розеток.
Ну вот в принципе и все. И как всегда по традиции ролик о последовательном и параллельном подключении ламп
Теперь я думаю, у Вас не должно возникнуть проблем с последовательным и параллельным соединением ламп.
Удачи!
Источник: https://sesaga.ru/posledovatelnoe-i-parallelnoe-soedinenie-lamp.html
Последовательное и параллельное соединение сопротивлений
Здравствуйте.
Сегодня мы будем рассматривать последовательное и параллельное соединение сопротивлений. Тема очень интересная и касающаяся нашей повседневной жизни. Как правило, именно с этой темы начинается проектирование электропроводки любого объекта. В прочем, обо всём по порядку.
Для начала разберемся почему «сопротивление». Синонимами этого определения могут быть: нагрузка или резистор. Поскольку мы с вами говорим об электрической сети, стало быть, по проводам протекает ток. Как бы хорошо не протекал ток по проводам, и из каких бы материалов не изготавливали провода, все равно на ток действует, своего рода сила трения.
То есть, ток встречает некое сопротивление и в зависимости от материала, поперечного сечения и длины провода это сопротивление сильнее или слабее. Так, в русском языке был принят термин «сопротивление», обозначающий некий элемент цепи, создающий ощутимое препятствие для прохождения тока, а позже появился народный термин «нагрузка», то есть, нагружающий элемент, а из английского языка пришел термин «резистор». С понятиями разобрались, теперь можно приступать к практике.
А начнём, пожалуй, с параллельного соединения сопротивлений просто потому, что мы им пользуемся практически повсеместно.
Параллельное соединение сопротивлений
При параллельном подключении все сопротивления подключаются началами к одной точке источника питания, а концами к другой. Далеко ходить не будем, и посмотрим вокруг себя.
Фен, утюг, стиральная машинка, тостер, микроволновка и любой другой электрический прибор имеют вилку с двумя рабочими концами и одним защитным (заземлением). Напряжение в розетке это наш источник питания.
Сколько бы электроприборов мы не включили в сеть – мы их все включаем параллельно к одному источнику питания. Давайте нарисуем схему, чтобы стало более понятно.
Сколько бы эту схему не добавилось потребителей – ровным счётом ничего не меняется. Один конец электроприбора подключается к нулевой шине, а второй к фазе. Теперь несколько преобразуем схему:
Теперь перед нами три сопротивления:
Утюг 2,2 кВт – R1 (22 Ом);
Плита 3,5 кВт – R2 (14 Ом);
Лампочка 100 Вт – R3 (484 Ом).
Таковы реальные значения сопротивления этих потребителей электрическому току. Включаем по очереди наши потребители в сеть, и что происходит со счетчиком? Правильно, он начинает быстрее считать деньги в нашем кошельке.
Теперь вспоминаем закон Ома, который гласит, что сила тока обратно пропорциональна сопротивлению и понимаем, что чем меньше сопротивление, тем выше сила тока. А чтобы еще проще было понять, что происходит, представьте себе концертный зал с тремя разными по габаритам выходами и толпой людей.
Чем больше по габаритам открывается дверь, тем больше человек одновременно могут через нее пройти, а чем больше откроется дверей, тем больше это увеличит пропускную способность. Ну а теперь перейдём к формулам.
К каждому сопротивлению приложено одно и то же напряжение – 220 вольт.
Из схемы и из практики видим, что токи складываются в один общий, следовательно, получаем следующее уравнение:
Если внимательно присмотритесь к уравнению, то заметите, что верхняя часть уравнения у нас неизменна и её можно принять за единицу, получив следующую формулу:
Ещё есть частная формула для расчёта двух параллельно соединенных сопротивлений:
Ну и давайте на практике сделаем расчёт.
И получим общее сопротивление 8,407 Ом.
В предыдущей статье я рассматривал баланс мощности и давайте его проверим.
Мощность цепи будет:
Считаем наши мощности: 2000+3500+100=5600, что почти равно 5757, такая большая погрешность обусловлена тем, что я округлил значения сопротивлений до целых чисел.
Какие можно сделать выводы. Как видите, общее сопротивление (его ещё называют эквивалентным) всегда будет меньше, чем самое малое сопротивление цепи. В нашем случае это плита с сопротивлением 14 Ом и эквивалентное 8,4 Ом. Оно и понятно.
Помните пример с дверями в концертном зале? Сопротивление можно назвать пропускной способностью. Так вот общее количество выходящих людей (электронов) из зала будет в сумме больше, чем пропускная способность каждой отдельно взятой двери. То есть, количество тока увеличивается.
Другими словами, для тока каждое из сопротивлений будет еще одной дверью, через которые он может протекать.
Последовательное соединение сопротивлений
При последовательном соединении конец одного сопротивления соединяется с другим. Типовой пример такого соединения – новогодняя гирлянда.
Насколько известно из школьного курса физики по замкнутому контуру протекает только один ток. Таким образом, что мы имеем:
Лампочка 200 ватт – R1 (242 Ом)
Лампочка 100 ватт – R2 (484 Ом)
Лампочка 50 ватт – R3 (968 Ом)
Снова вернёмся к аллегории и представим концертный зал, но только в этот раз из него будет вести длинный коридор с тремя дверями. Теперь у тока (людей) только один путь последовательно пройти от одной двери к другой. Для решения этой задачи нам придется отталкиваться от напряжения. Исходя из того, что сумма на источнике питания равна сумме падений напряжений на сопротивлениях получим следующую формулу:
Отсюда следует:
Делим обе части уравнения на общую величину приходим к выводу, что при последовательном соединении для получения эквивалентного сопротивления цепи надо суммировать все сопротивления этой цепи:
Проверяем. R=242+484+968=1694 Ом
Как видим, баланс мощности почти сошёлся. А теперь внимание на одну особенность, которая ещё раз раскроет понятие «сопротивление». Обратите внимание, что наибольшая мощность у нас будет на самой слабой лампочке:
Казалось бы, должно быть все наоборот, более мощная лампочка должна светить ярче. Возвращаемся к нашей аллегории. Как вы думаете, где будет давка сильнее возле широкой двери или возле узкой? Где будет горячее? Конечно же, возле узкой двери возникнет давка, а там где давка, там будет горячо, потому что люди будут стараться проложить себе путь побыстрее. В токе роль людей выполняют электроны.
Вот такой вот парадокс возникает при включении в последовательную цепь резисторов разного номинала и именно поэтому в гирляндах стараются применять одинаковые лампочки. Теперь, зная принципы последовательного соединения сопротивлений, вы можете рассчитать любую гирлянду. Например, у вас имеются автомобильные лампы на 12 вольт. Зная, что общее напряжение равно сумме падений напряжений нам достаточно 220 вольт разделить на 12 вольт и получим 18,3 лампы.
То есть, если взять 18 или 19 одинаковых 12 вольтовых ламп и соединить последовательно, то их можно включить в 220 вольт и они не перегорят.
Подведём итоги
При параллельном соединении сопротивлений эквивалентное сопротивление уменьшается (концертный зал опустошается в три раза быстрее, грубо говоря, люди разбегаются по трем коридорам), а при последовательном соединении сопротивление увеличивается (как бы люди не хотели быстрее покинуть зал, делать им это придется только по одному коридору и чем коридор уже, тем больше сопротивление он создает).
Источник: https://uelektrika.ru/soedinenie-yelektroprovodki/posledovatelnoe-i-parallelnoe-soe/
Параллельное соединение резисторов
> Теория > Параллельное соединение резисторов
Параллельные соединения резисторов, формула расчёта которых выводится из закона Ома и правил Кирхгофа, являются наиболее распространённым типом включения элементов в электрическую цепь. При параллельном соединении проводников два или несколько элементов объединяются своими контактами с обеих из сторон соответственно. Подключение их к общей схеме осуществляется именно этими узловыми точками.
Особенности включения
Включённые таким образом проводники нередко входят в состав сложных цепочек, содержащих, помимо этого, последовательное соединение отдельных участков.
Для такого включения типичны следующие особенности:
- Общее напряжение в каждой из ветвей будет иметь одно и то же значение;
- Протекающий в любом из сопротивлений электрический ток всегда обратно пропорционален величине их номинала.
В частном случае, когда все включённые в параллель резисторы имеют одинаковые номинальные значения, протекающие по ним «индивидуальные» токи также будут равны между собой.
Расчёт
Параллельное соединение резисторов
Сопротивления ряда соединённых в параллель проводящих элементов определяются по общеизвестной форме расчёта, предполагающей сложение их проводимостей (обратных сопротивлению величин).
Протекающий в каждом из отдельных проводников ток в соответствие с законом Ома, может быть найден по формуле:
I= U/R (одного из резисторов).
После ознакомления с общими принципами обсчёта элементов сложных цепочек можно перейти к конкретным примерам решения задач данного класса.
Пример №1
Нередко для решения стоящей перед конструктором задачи требуется путём объединения нескольких элементов получить в итоге конкретное сопротивление. При рассмотрении простейшего варианта такого решения допустим, что общее сопротивление цепочки из нескольких элементов должно составлять 8 Ом. Этот пример нуждается в отдельном рассмотрении по той простой причине, что в стандартном ряду сопротивлений номинал в 8 Ом отсутствует (есть только 7,5 и 8,2 Ом).
Решение этой простейшей задачи удаётся получить за счёт соединения двух одинаковых элементов с сопротивлениями по 16 Ом каждое (такие номиналы в резистивном ряду существуют). Согласно приводимой выше формуле общее сопротивление цепочки в этом случае вычисляется очень просто.
Из неё следует:
16х16/32=8 (Ом), то есть как раз столько, сколько требовалось получить.
Таким сравнительно простым способом удаётся решить задачу формирования общего сопротивления, равного 8-ми Омам.
Пример №2
В качестве ещё одного характерного примера образования требуемого сопротивления можно рассмотреть построение схемы, состоящей из 3-х резисторов.
Общее значение R такого включения может быть рассчитано по формуле последовательного и параллельного соединения в проводниках.
В соответствии с указанными на картинке значениями номиналов, общее сопротивление цепочки будет равно:
1/R = 1/200+1/220+1/470 = 0,0117;
R=1/0,0117 = 85,67Ом.
В итоге находим суммарное сопротивление всей цепочки, получаемой при параллельном соединении трёх элементов с номинальными значениями 200, 240 и 470 Ом.
Важно! Указанный метод применим и при расчёте произвольного числа соединенных в параллель проводников или потребителей.
Также необходимо отметить, что при таком способе включения различных по величине элементов общее сопротивление будет меньше, чем у самого малого номинала.
Расчёт комбинированных схем
Параллельное соединение проводников
Рассмотренный метод может применяться и при расчёте сопротивления более сложных или комбинированных схем, состоящих из целого набора компонентов. Их иногда называют смешанными, поскольку при формировании цепочек используются сразу оба способа. Смешанное соединение резисторов представлено на размещенном ниже рисунке.
В приведённом выше примере требуется посчитать суммарное значение номиналов цепи, состоящей из трех резисторов.
Для упрощения расчета сначала разбиваем все резисторы по типу включения на две самостоятельные группы. Одна из них представляет собой последовательное соединение, а вторая – имеет вид подключения параллельного типа.
Из приведённой схемы видно, что элементы R2 и R3 соединяются последовательно (они объединены в группу 2), которая, в свою очередь, включена в параллель с резистором R1, принадлежащим группе 1.
Для элементов из группы 2 значение общего сопротивления находится как сумма R2 и R3:
R (2+3) = R2 + R3.
Для получения окончательного результата приводим схему к виду, получаемому при параллельном соединении двух сопротивлений. После этого суммарное значение для всей схемы в целом вычисляется согласно уже рассмотренной ранее формуле.
В заключение отметим, что для проведения расчётных операций, относящихся к категории сложных соединений, можно воспользоваться теми же методиками. В их основу заложены всё те же закон Ома и правила Кирхгофа, известные ещё со школьной скамьи. Главное – это грамотно распорядиться всеми описанными выше формулами.
Последовательное и параллельное соединение аккумуляторов
Источник: https://elquanta.ru/teoriya/parallelnoe-soedinenie-rezistorov.html
Закон Ома для участка цепи. Последовательное и параллельное соединение проводников. 10 класс. Физика. — Объяснение нового материала
Сила тока на участке цепи прямо пропорциональна напряжению на этом участке и обратно пропорциональна сопротивлению участка.
Закон Ома оказался справедливым не только для металлов, но и для растворов электролитов. Сформулированный закон имеет место для так называемого однородного участка цепи – участка, не содержащего источников тока.
Математическая запись закона Ома проста, как и его формулировка, но экспериментально подтвердить эту зависимость очень трудно. Сила тока, протекающая по участку цепи, мала. Поэтому используют достаточно чувствительные приборы. Г. Ом изготовил чувствительный прибор для измерения силы тока, а в качестве источника тока использовал термопару. Действие амперметра и вольтметра основано на применение закона Ома для участка цепи. Угол поворота стрелки прибора пропорционален силе тока.
Из математической записи закона Ома:
можно выразить напряжение :
и сопротивление проводника:
.
Таким образом, закон Ома связывает три параметра, характеризующих постоянный электрический ток, проходящий по проводнику, и позволяет находить любой из них, если известны два других.
Закон Ома имеет границы применимости и выполняется только в том случае, когда при прохождении тока температура заметно не меняется. На вольт–амперной характеристике лампы накаливания видно, что график сильно искривляется при напряжении выше 10В, значит, закон Ома выше этого напряжения применять нельзя.
Также нельзя говорить, что сопротивление проводника зависит от напряжения и силы тока в цепи. Сопротивление участка цепи зависит от свойств проводника: длины, площади поперечного сечения и материала, из которого состоит проводник.
где l-длина проводника, s-его площадь поперечного сечения.
ρ –удельное сопротивление проводника – это физическая величина, характеризующая зависимость сопротивления проводника от материала, из которого он изготовлен.
Удельное сопротивление показывает, каким сопротивлением обладает сделанный из этого вещества проводник длиной 1м и площадью поперечного сечения 1м2 .
Из формулы видно, что единицей измерения в системе СИ является Ом·м. Но так как площадь поперечного сечения проводника достаточно мала, используют единицы измерения
при вычислении площадь поперечного сечения проводника следует выражать в мм2.
В заключении хочется заметить, что Ом начал свои опыты, когда был учителем физики в гимназии. В своих экспериментах Ом брал куски проволоки одинакового диаметра, но разного материала и изменял их длину таким образом, чтобы в цепи сила тока имела одинаковое значение. Находящаяся рядом магнитная стрелка отклонялась при прохождении тока в цепи. Установив связь между напряжением и силой тока, Г. Ом вывел один из основных законов постоянного тока.
Последовательное соединение проводников
Электрические цепи, с которыми приходится иметь дело на практике, обычно состоят не из одного приёмника электрического тока, а из нескольких различных, которые могут быть соединены между собой по-разному. Зная сопротивление каждого и способ их соединения, можно рассчитать общее сопротивление цепи.
На рисунке а изображена цепь последовательного соединения двух электрических ламп, а на рисунке б — схема такого соединения. Если выключать одну лампу, то цепь разомкнётся и другая лампа погаснет.
Рис. Последовательное включение лампочек и источников питания
Мы уже знаем, что при последовательном соединении сила тока в любых частях цепи одна и та же, т. е.
I = I1 = I2
А чему равно сопротивление последовательно соединённых проводников?
Соединяя проводники последовательно, мы как бы увеличиваем длину проводника. Поэтому сопротивление цепи становится больше сопротивления одного проводника.
Последовательное соединение проводников
Общее сопротивление цепи при последовательном соединении равно сумме сопротивлений отдельных проводников (или отдельных участков цепи):
R = R1 + R2
Напряжение на концах отдельных участков цепи рассчитывается на основе закона Ома:
U1 = IR1, U2 = IR2.
Из приведённых равенств видно, что напряжение будет большим на проводнике с наибольшим сопротивлением, так как сила тока везде одинакова.
Полное напряжение в цепи при последовательном соединении, или напряжение на полюсах источника тока, равно сумме напряжений на отдельных участках цепи:
U = U1 + U2.
Это равенство вытекает из закона сохранения энергии. Электрическое напряжение на участке цепи измеряется работой электрического тока, совершающейся при прохождении по участку цепи электрического заряда в 1 Кл. Эта работа совершается за счёт энергии электрического поля, и энергия, израсходованная на всём участке цепи, равна сумме энергий, которые расходуются на отдельных проводниках, составляющих участок этой цепи.
Все приведённые закономерности справедливы для любого числа последовательно соединённых проводников.
Пример 1. Два проводника сопротивлением R1 = 2 Ом, R2 = 3 Ом соединены последовательно. Сила тока в цепи I = 1 А. Определить сопротивление цепи, напряжение на каждом проводнике и полное напряжение всего участка цепи.
Запишем условие задачи и решим её.
ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ
Расчет параметров электрической цепи
при параллельном соединении сопротивлений:
Источник: https://www.kursoteka.ru/course/3296/lesson/11139/unit/27691
Соединение резисторов
Это такое соединение, при котором все элементы идут один за одним без разветвлений.
Свойства последовательного соединения
1. Ток во всех резисторах одинаков- I1 = I2 = I3;
2. Общее напряжение цепи равно сумме напряжений на всех резисторах- U=U1 + U2 + U3;
3.Сопротивление по отношению к входным зажимам называется входным сопротивлением и равно сумме сопротивлений участков — Rвх= R1 + R2 + R3;
4. Чем больше сопротивление участка, тем больше на нём падает напряжение-.
ПАРАЛЛЕЛЬНОЕ Соединение резисторов
Это такое соединение, при котором все начала элементов соединяются в одну точку, а все концы в другую и к этим точкам подводится напряжение.
Свойства параллельного соединения резистора:
1. Общее напряжение цепи равно напряжению на каждом участке-
U = U1 = U2 = U3
2. Общий ток цепи равен сумме токов на всех участках- I = I1 + I2 + I3
3. Чтобы найти входное сопротивление, рассчитывают вначале величину обратную входному сопротивлению
— проводимость (G)
Общая проводимость цепи равна сумме проводимостей на каждом участке.
G = G1 + G2 + G3
4.Чем больше сопротивление участка, тем меньше ток, протекающий на нем.
При параллельном соединении двух резисторов формулу входного сопротивления можно преобразовать
1.
2. Если известен общий ток, то можно найти ток ветви, умножив общий ток на сопротивление противоположной ветви и разделить на сумму сопротивлений ; .
Тестовые задания:
| Задание | Варианты ответов |
| 1.Являются ли при последовательном соединении резисторов напряжения участков пропорционально сопротивлениям этих участков. | Да; Нет. |
| 2.Являются ли при параллельном соединении резисторов токи ветвей пропорциональны сопротивлениям этих ветвей. | Да; Нет. |
| 3.Укажите по какому из приведенных математических выражений нельзя рассчитать входное сопротивление двух параллельно соединенных резисторов. | а) ; б); в) ; г) |